Longitudinal changes in youth baseball batting based on body rotation and separation | BMC Sports sciences, medicine and rehabilitation
Attendees
We initially recruited 230 junior baseball players from six teams in Tokyo, Japan in April 2018. The inclusion criteria were males between 6 and 12 years old. The exclusion criteria were injury and illness that prevented the participant from taking measurements. Participants were divided into age groups during the baseball season according to little league eligibility rules – players were classified by age as of July 31 of a given year. Subsequently, the period up to and including July 31 of the second year of primary school was defined as Under 8 (U8), and then the period was divided by year up to and including U13. They played and practiced baseball at least twice a week (Saturday and Sunday) for 3 to 6 hours. Before the study, all participants completed a data questionnaire that asked for the following information: birth, age when they first started playing baseball, and the side they hit. In addition, all participants and their guardians were given a detailed explanation of the experimental procedures and risks of the study before any measurements were taken. In addition, written informed consent was obtained from all participants and their guardians who agreed to the study. This study was approved by the Ethics Committee of Waseda University (No. 2018 − 208).
Batting procedure
Testing was conducted between 9:00 AM and 4:00 PM on an outdoor baseball field maintained under standard environmental conditions. In addition, testing took place between January and March, spread over 4 to 6 days per season. First, we measured the participant’s height and weight while wearing clothes. Then, without shoes on, height was measured to the nearest 0.1 cm without shoes on using a stadiometer (YG200DN, Yagami Co., Nagoya, Japan); and weight was measured to the nearest 0.1 kg using a digital scale (BC622, TANITA Co., Tokyo, Japan). The hitting test was then performed after simple warm-up exercises including dynamic stretching, jogging, light throwing and swinging for approximately 20 minutes. Each participant received unreflected white markers on the top of the head, both lateral acromion points, and the anterior and superior iliac spines. The trial involved toss batting with an automatic toss machine (FTM-240; Field Force Company, China). The toss machine was placed 0.7 m from the center of home plate on the opposite side of the batter and 1.1 m toward the pitcher; it was positioned to launch diagonally in front of the batter. The height of the throwing machine was adjusted to the participant’s height as follows: 45% of the height minus 52.5 cm. Then, after one practice trial, actual testing was performed twice and the hitting motion was recorded at 240 Hz with three high-speed cameras (Ex-100PRO, Casio Co., Tokyo Japan) placed on the side, back, and front of the hitter (oblique). The environment of the impact test environment was shown in Figure 1.
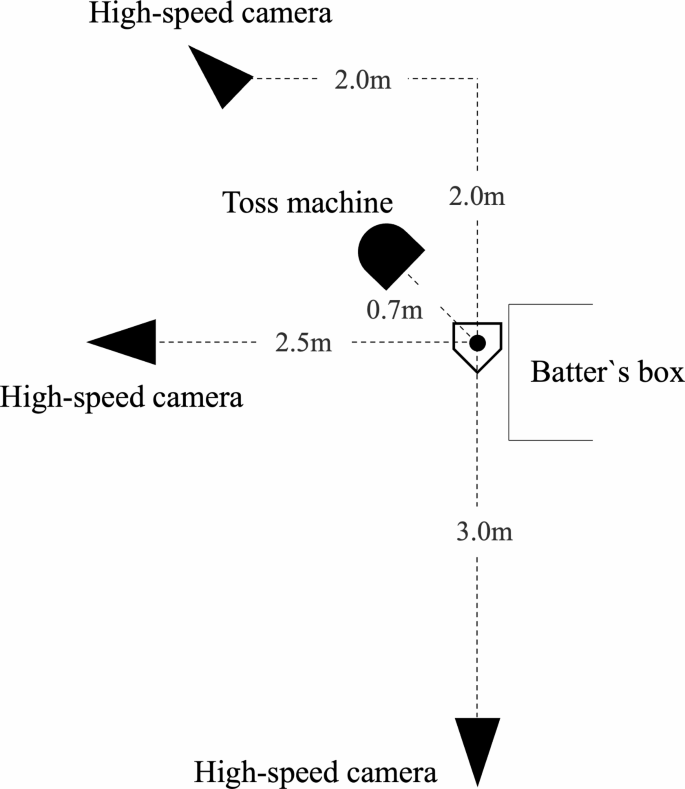
Environment of batting test (in case of left-handed batsman)
In addition, swing speed, a component of hitting performance, was measured using a Zepp sensor (ZEP-BT-000002; Zepp Company, Cupertino, California, USA), which has been shown to have high reliability (ICC, 0. 88). [13]and indicated that it correlates moderately to strongly with data analyzed by 3D motion tracking [14]. Participants were allowed to retry the hitting test if they missed the ball while swinging or made timing errors. During the batting test, participants used the bat they would normally use in baseball practice and games, and consistently used the same bat throughout their trials. Data were collected from the highest swing speed test.
Variables
The rotation angles of the head, trunk, pelvis and arm direction in the horizontal plane during the stroke movement and the separation angle between each segment, the amount of head movement and the step width were analyzed by manual digitizing using a motion analysis. system (Frame-Dias V; DKH, Tokyo, Japan). In addition, we visualized the body markers attached to the head, both the lateral acromion points, the anterior and superior iliac spines, the nose, the toes and the midpoint between both hands on the screen using a digital format. Then, three-dimensional coordinates were obtained using the direct linear transformation method [15], and the right orthogonal reference frame was defined as the X-axis, Y-axis, and Z-axis. The Y axis was directed from the pitcher’s mound to home plate, and the Z axis indicated a vertical direction (bottom to top). Furthermore, the X-axis was defined as the cross product of the Y-axis and the Z-axis. For calibration, posts with nine markers (from 0 to 2.0 m at 25 cm intervals) were placed vertically in a 4 x 4 grid at 40 cm intervals (the standard errors were as follows: x = 0.22 cm; y = 0.28 cm; z = 0.34 centimeter). From the beginning to the end of the at bat, a recording of the calibration points was performed using the three high-speed cameras. The analysis data was collected at five points: stance, load, foot contact, front swing and ball contact. Stance and foot contact were defined as the point of the toe of the stepping leg on the Z axis at which the Z axis value began to increase in a positive direction. In addition, load and foreswing were defined as the midpoints between stance and foot contact and between foot contact and ball contact, respectively.
All rotation angles were calculated using values corresponding to spaces in global coordinates, because batting is an operation initiated by responding to a thrown ball and is defined as the projected angle on the horizontal plane relative to the X axis ( Fig. 2). Additionally, the rotation angles were set as positive/negative relative to the pitcher/catcher.
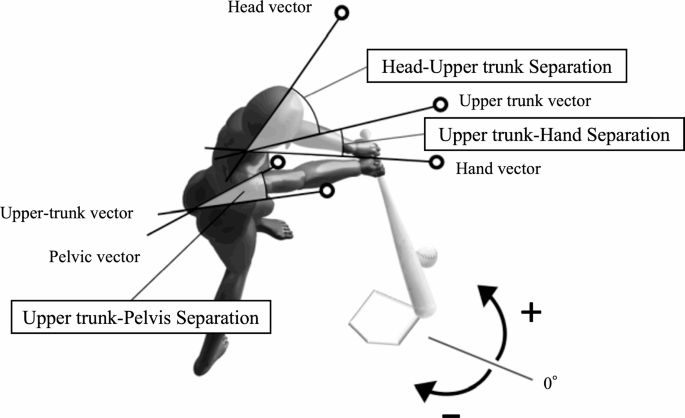
Definitions of rotation and separation variables
The variables analyzed in this study and their definitions are as follows:
Head rotation: the angle between the head vector (top of the head to the nose) and the X-axis.
Upper torso rotation: the angles between the upper torso vector (through the center of both acromions and perpendicular to the line joining both points) and the X-axis.
Arm direction: the angle between the hand vector (center of both acromions to a point between both hands) and the X-axis.
In addition, the separation angle was expressed as the difference between each rotation angle, and the separation between head and upper trunk was calculated by subtracting the head rotation from the upper trunk rotation. In addition, the separation between the torso and arms was calculated by subtracting the rotation of the upper torso from the arm direction. The upper to pelvic separation was calculated by subtracting the rotation of the upper torso from the rotation of the pelvis. The linear head movement distance (head movement) from stance to foot contact and foot contact to ball contact was calculated as the resulting displacement of the top of the head. Finally, stance widths during stance and foot contact were calculated as the distance between the toes.
static analysis
Statistical power analysis was performed to estimate the sample size. For this study, we needed more than twelve players to perform a comparison between the three groups with 80% power, an alpha of 0.05. and a partial η of 0.14. Seventy-seven baseball players who met inclusion criteria completed three measurements over three seasons. Of these, 17 players formed group 1 (U8 to U10) and 13 players formed group 2 (U11 to U13) (Fig. 3).
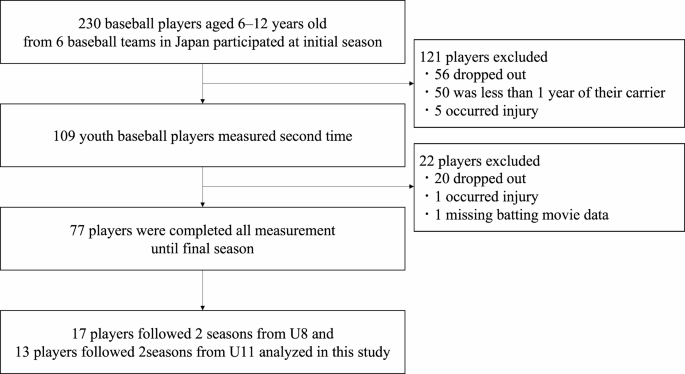
Flowchart of exclusion criteria and final participants
Descriptive statistics (mean ± standard deviation) were performed. After confirming that all data were normally distributed using the Kolmogorov-Smirnov test and confirming homoscedasticity using the Levene test, we performed a one-way analysis of variance (ANOVA) to determine chronological age, height, body weight, years of competition, rotation, and separation comparable. angles, swing speed, head movement and step width at stances, load, foot contact, pre-swing and ball contact between the initial, second and final measurements over three seasons. Additionally, we performed multiple comparisons of the means of the controlled variables using the Bonferroni test. Partial η2 was calculated for the effect size of the one-way ANOVA, with values of ≥ 0.01 to < 0.06, ≥ 0.06 to < 0.14, and ≥ 0.14, indicating small, medium, and large effects, respectively [16]. Finally, the alpha level was set at 0.05 and all statistical analyzes were performed using SPSS Statistics 27.0 (IBM, Armonk, New York, USA).